[Qt OpenGL教程主页] [下一课：显示列表]

旗的效果（波动纹理）

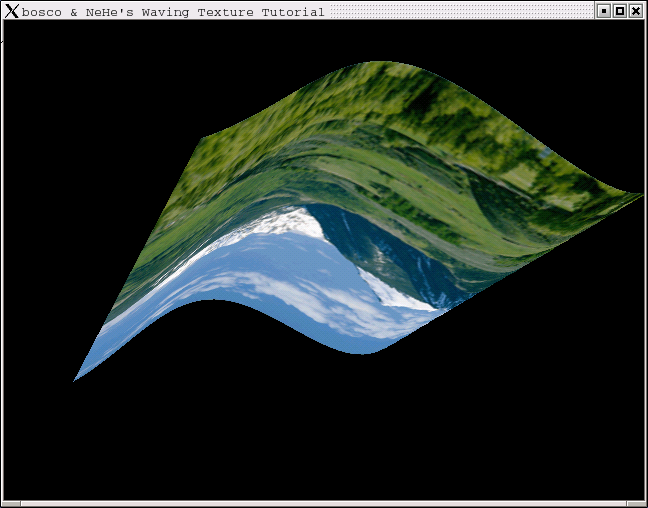
大家好！对那些想知道我在这里作了些什么的朋友，您可以先按文章的末尾所列出的链接，下载我那毫无意义的Demo看看先！我是bosco，我将尽我所能教您来实现一个以正弦波方式运动的图象。这一课基于NeHe的教程第六课，当然您至少也应该学会了一至六课的知识。您需要下载源码压缩包，并将压缩包内带的data目录连其下的位图一起释放至您的代码目录下。或者使用您自己的位图，当然它的尺寸必须适合OpenGL纹理的要求。

NeHeWidget类

（由nehewidget.h展开。）

class NeHeWidget : public QGLWidget
{
    Q_OBJECT

public:
    
  NeHeWidget( QWidget* parent = 0, const char* name = 0, bool fs = false );
  ~NeHeWidget();

protected:

  void initializeGL();
  void paintGL();
  void resizeGL( int width, int height );
  
  void keyPressEvent( QKeyEvent *e );
  void loadGLTextures();
  void timerEvent( QTimerEvent * );

这些函数前几课中都提到过了。

protected:

  bool fullscreen;
  
  GLfloat xRot, yRot, zRot;
  GLfloat hold;
  GLuint texture[1];
  
  float points[45][45][3];
  int wiggle_count;
};

我们将使用points数组来存放网格各顶点独立的(x,y,z)坐标。这里网格由45×45点形成，换句话说也就是由44格×44格的小方格子依次组成了。wiggle_count用来指定纹理波浪的运动速度，每3帧一次看起来很不错。变量hold将存放一个用来对旗形波浪进行光滑的浮点数。

（由nehewidget.cpp展开。）

#include <math.h>

因为我们在程序中要使用到sin和cos两个三角函数，所以我们需要包含math.h这个头文件。

NeHeWidget::NeHeWidget( QWidget* parent, const char* name, bool fs )
    : QGLWidget( parent, name )
{
  xRot = yRot = zRot = 0.0;
  hold = 0.0;
  
  wiggle_count = 0;
  
  fullscreen = fs;
  setGeometry( 0, 0, 640, 480 );
  setCaption( "bosco & NeHe's Waving Texture Tutorial" );

  if ( fullscreen )
    showFullScreen();

  startTimer( 5 );
}

我们需要在构造函数中给各个变量赋初值。startTimer()函数我们在第九课中已经讲过了。

void NeHeWidget::loadGLTextures()
{
  QImage tex, buf;
  if ( !buf.load( "./data/Tim.bmp" ) )
  {
    qWarning( "Could not read image file, using single-color instead." );
    QImage dummy( 128, 128, 32 );
    dummy.fill( Qt::green.rgb() );
    buf = dummy;
  }
  tex = QGLWidget::convertToGLFormat( buf );
  
  glGenTextures( 1, &texture[0] );
  
  glBindTexture( GL_TEXTURE_2D, texture[0] );
  glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR );
  glTexParameteri( GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR );
  glTexImage2D( GL_TEXTURE_2D, 0, 3, tex.width(), tex.height(), 0,
      GL_RGBA, GL_UNSIGNED_BYTE, tex.bits() );
}

loadGLTextures()函数就是用来载入纹理的。

void NeHeWidget::initializeGL()
{
  loadGLTextures();

  glEnable( GL_TEXTURE_2D );
  glShadeModel( GL_SMOOTH );
  glClearColor( 0.0, 0.0, 0.0, 0.5 );
  glClearDepth( 1.0 );
  glEnable( GL_DEPTH_TEST );
  glDepthFunc( GL_LEQUAL );
  glHint( GL_PERSPECTIVE_CORRECTION_HINT, GL_NICEST );
  glPolygonMode( GL_BACK, GL_FILL );
  glPolygonMode( GL_FRONT, GL_LINE );

上面的代码指定使用完全填充模式来填充多边形区域的背面（或者叫做后表面吧）。相反，多边形的正面（前表面）则使用轮廓线填充了。这些方式完全取决于您的个人喜好。并且与多边形的方位或者顶点的方向有关。详情请参考Red Book。这里我顺便推销一本推动我学习OpenGL的好书－Addison-Wesley出版的《Programmer's Guide to OpenGL》。个人以为这是学习OpenGL的无价之宝。

  for ( int x = 0; x < 45; x++ )
  {
    for ( int y = 0; y < 45; y++ )
    {
      points[x][y][0] = float( ( x/5.0 ) - 4.5 );
      points[x][y][1] = float( ( y/5.0 ) - 4.5 );
      points[x][y][2] = float( sin( ( ( ( x/5.0 ) * 40.0 )/360.0 ) * 3.141592654 * 2.0 ) );
    }
  }

这里感谢Graham Gibbons关于使用整数循环变量消除波浪间的脉冲锯齿的建议。

上面的两个循环初始化网格上的点。使用整数循环可以消除由于浮点运算取整造成的脉冲锯齿的出现。我们将x和y变量都除以5，再减去4.5。这样使得我们的波浪可以“居中”（这样计算所得结果将落在区间[-4.5，4.5]之间）。

点[x][y][2]最后的值就是一个sin函数计算的结果。sin()函数需要一个弧度参变量。将float_x乘以40.0，得到角度值。然后除以360.0再乘以PI，乘以2.0，就转换为弧度了。

}

void NeHeWidget::paintGL()
{
  int x, y;
  float float_x, float_y, float_xb, float_yb;

x、y是循环变量，float_x、float_y、float_xb、float_yb是用来将旗形的波浪分割成很小的四边形。

  glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
  glLoadIdentity();
  
  glTranslatef( 0.0, 0.0, -12.0 );

  glRotatef( xRot, 1.0, 0.0, 0.0 );
  glRotatef( yRot, 0.0, 1.0, 0.0 );
  glRotatef( zRot, 0.0, 0.0, 1.0 );

  glBindTexture( GL_TEXTURE_2D, texture[0] );

  glBegin( GL_QUADS );

开始绘制四边形。

    for ( x = 0; x < 44; x++ )
    {

沿X平面0-44循环（45点）

      for ( y = 0; y < 44; y++ )
      {

沿Y平面0-44循环（45点）

        float_x = float(x)/44.0;
        float_y = float(y)/44.0;
        float_xb = float(x+1)/44.0;
        float_yb = float(y+1)/44.0;

上面我们使用4个变量来存放纹理坐标。每个多边形（网格之间的四边形）分别映射了纹理的1/44 x 1/44部分。循环首先确定左下顶点的值，然后我们据此得到其他三点的值。

        glTexCoord2f( float_x, float_y );
        glVertex3f( points[x][y][0], points[x][y][1], points[x][y][2] );

        glTexCoord2f( float_x, float_yb );
        glVertex3f( points[x][y+1][0], points[x][y+1][1], points[x][y+1][2] );

        glTexCoord2f( float_xb, float_yb );
        glVertex3f( points[x+1][y+1][0], points[x+1][y+1][1], points[x+1][y+1][2] );

        glTexCoord2f( float_xb, float_y );
        glVertex3f( points[x+1][y][0], points[x+1][y][1], points[x+1][y][2] );

上面四个坐标分别为左下、左上、右上、右下。

上面几行使用glTexCoord2f()和 glVertex3f()载入数据。提醒一点：四边形是逆时针绘制的。这就是说，您开始所见到的表面是背面。后表面完全填充了，前表面由线条组成。

如果您按顺时针顺序绘制的话，您初始时见到的可能是前表面。也就是说您将看到网格型的纹理效果而不是完全填充的。

      }
    }
  glEnd();

四边形绘制结束。

  if ( wiggle_count == 2 )
  {
    for ( y = 0; y < 45; y++ )
    {
      hold = points[0][y][2];
      for ( x = 0; x < 44; x++ )
      {
        points[x][y][2] = points[x+1][y][2];
      }
      points[44][y][2] = hold;
    }
    wiggle_count = 0;
  }

  wiggle_count++;

上面所作的事情是先存储每一行的第一个值，然后将波浪左移一下，是图象产生波浪。存储的数值挪到末端以产生一个永无尽头的波浪纹理效果。然后重置计数器 wiggle_count以保持动画的进行。

上面的代码由NeHe（2000年2月）修改过，以消除波浪间出现的细小锯齿。

 
  xRot += 0.3;
  yRot += 0.2;
  zRot += 0.4;

标准的NeHe旋转增量:)。

}

void NeHeWidget::timerEvent(QTimerEvent*)
{
  updateGL();
}

void NeHeWidget::keyPressEvent( QKeyEvent *e )
{
  switch ( e->key() )
  {
  case Qt::Key_F2:
    fullscreen = !fullscreen;
    if ( fullscreen )
    {
      showFullScreen();
    }
    else
    {
      showNormal();
      setGeometry( 0, 0, 640, 480 );
    }
    update();
    break;
  case Qt::Key_Escape:
    close();
  }
}

现在编译并运行程序，您将看到一个漂亮的位图波浪。除了嘘声一片之外，我不敢确信大家的反应。但我希望大家能从这一课中学到点什么。如果您有任何问题或者需要澄清的地方，请随便联络我。感谢大家！

本课程的源代码。

[Qt OpenGL教程主页] [下一课：显示列表]